|
|

#De la justification des matrices |
|
|
Tous
ces petits morceaux de cuivre ainsi frappés,
que l'on nomme matrices,
ont besoin d'être justifiés pour acquérir toute leur perfection.
Pour cela,
on lime toutes les faces du cuivre avec tant de précision,
qu'il n'y ait pas une seule matrice plus enfoncée que l'autre,
ni qui porte plus de cuivre aux deux côtés,
non #plus
que de la lettre au pied de la matrice.
Elles doivent être justifiées de façon qu'en entrant les unes après les autres dans
l'endroit du moule destiné à les recevoir,
elles rendent chacune leur lettre,
sur la fonte,
dans le degré de justesse et de perfection où elles doivent se trouver pour
l'impression ; ce qu'on appelle justifier à registre arrêté. |
|
|
On justifie
d'abord la lettre m dans le degré de profondeur que l'on veut donner à l'œil de la lettre,
et de la largeur convenable : cette première matrice justifiée servira de règle pour les autres.
On fond sur cette matrice trois m,
que l'on met sur un petit instrument nommé justification,
et entre ces trois m on passe successivement toutes les lettres de la frappe,
à mesure que l'on justifie les matrices,
pour les y conformer tant pour la hauteur en papier,
que pour l'approche et la ligne. |
|
|
On prend
douze ou quinze matrices pour les justifier à la fois,
afin d'accélérer l'ouvrage ; après qu'elles sont dégrossies,
on fond une lettre sur chacune desdites matrices ; on les frotte
sur les deux flancs et sur le corps du côté du cran ; cela se fait sur
une pierre à frotter ou
#sur une lime large
et bien droite ; puis,
avec un petit couteau en forme de canif,
on enlève l'excédent de la cassure du jet à une de ces lettres,
on la met entre les trois m,
et on pose sur ces quatre lettres un petit niveau nommé jeton.
Si la lettre que l'on vient de mettre se trouve plus haute que les modèles,
c'est une marque qu'elle est trop enfoncée dans le cuivre :
on lime donc la surface de la matrice à peu près d'autant que l'œil paraît être trop
enfoncé ; mais il faut le faire avec connaissance de cause,
car il arrive quelquefois que le poinçon n'ayant pas toujours été tenu d'aplomb sur la matrice,
a été frappé un peu plus d'un coin que de l'autre.
Pour s'en assurer,
on pose une équerre appuyée d'un bout sur la tige de la lettre et l'autre sur l'œil.
Quand cet œil présente une partie plus élevée que l'autre,
c'est cette partie plus enfoncée dans la matrice qu'il faut limer davantage,
et en proportion du défaut.
En répétant peu à peu cette opération,
on parvient enfin à rendre toutes les lettres si égales entre elles pour la hauteur en papier,
que le jeton porte également sur les m et sur la lettre que l'on a mise entre elles. |
|
|
#Pour régler la hauteur
en papier,
on peut se servir encore de deux calibres différemment faits,
et qui me sont d'un grand usage.
Le premier est une lame de fer ou de laiton,
dans la longueur de laquelle est une entaille de dix lignes et demie,
qui est la hauteur que doivent avoir les caractères.
Le bout de ladite lame est dressé en forme du jeton.
Celui-ci,
que je nomme calibre fendu,
à cause de son entaille,
me sert pour voir,
d'un seul coup,
de combien la lettre est trop haute,
ou trop enfoncée dans la matrice,
et je la lime en proportion : par là j'évite l'opération beaucoup plus longue de couper au pied de la lettre l'excédent du jet avec le canif ; et ce n'est que lorsque la lettre commence à remplir l'entaille de ce calibre,
que,
pour plus grande sûreté,
je me sers du second que je nomme calibre mat ;
pour lors je coupe le pied de la lettre,
et j'en mesure la hauteur dedans.
Ce calibre de cuivre ou de fer est fait à peu près comme la justification.
Le côté étroit de l'équerre avec la platine forme une profondeur de dix lignes et demie :
j'ajoute à cela une petite branche mobile
#de même
hauteur ; la lettre étant serrée entre cette branche et celle de l'équerre,
on pose le jeton sur la surface de ce calibre,
à l'endroit où est la lettre,
et on voit avec la plus grande précision si cette lettre est au même niveau.
Ces calibres sont des mesures fixes pour régler la hauteur uniforme des caractères,
moins variable que les mm mises dans la justification,
qui peuvent intercepter par le pied quelques légères ordures,
ou s'affaiblir du côté de l'œil par le passage continuel du jeton. |
|
|
Mais comme la hauteur
des lettres n'est pas le seul point essentiel,
et que l'alignement de toutes ces lettres et leur approche respective ne
forment pas un objet moins intéressant,
il ne faut pas quitter la matrice que l'on n'y ait touché relativement à ces trois points.
Après avoir fini ce qui concerne la hauteur,
on regarde si la lettre qu'on a mise entre les m est bien de ligne avec elles :
s'il arrive qu'elle soit plus basse,
comme celle qu'on voit ici,
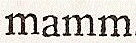 ,
ce qu'on appelle descendre en ligne,
c'est que la partie depuis l'œil jusqu'au pied de la matrice a trop de longueur ;
il faut donc en ôter.
Si au contraire elle monte plus haut que les
#traits des modèles,
comme dans cet exemple, ,
ce qu'on appelle descendre en ligne,
c'est que la partie depuis l'œil jusqu'au pied de la matrice a trop de longueur ;
il faut donc en ôter.
Si au contraire elle monte plus haut que les
#traits des modèles,
comme dans cet exemple,
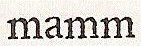 ,
ce qu'on nomme monter en ligne,
c'est que cette partie depuis l'œil jusqu'au bout de la matrice est trop courte :
on y remédie en donnant quelques coups de marteau sur ce bout de matrice ,
pour allonger le cuivre ; et comme il doit y avoir entre la lettre et les m
la même distance que les m entre eux,
ce que l'on nomme approche,
on doit ôter sur les flancs de la matrice en proportion de son trop d'épaisseur :
mais il faut encore le faire avec intelligence ; car dans le cas où une lettre qui
doit être droite et perpendiculaire incline un peu,
pour avoir été frappée de travers,
il faut la redresser en limant le cuivre sur le flanc de la matrice du côté opposé à l'endroit qui penche.
Dans cet exemple, ,
ce qu'on nomme monter en ligne,
c'est que cette partie depuis l'œil jusqu'au bout de la matrice est trop courte :
on y remédie en donnant quelques coups de marteau sur ce bout de matrice ,
pour allonger le cuivre ; et comme il doit y avoir entre la lettre et les m
la même distance que les m entre eux,
ce que l'on nomme approche,
on doit ôter sur les flancs de la matrice en proportion de son trop d'épaisseur :
mais il faut encore le faire avec intelligence ; car dans le cas où une lettre qui
doit être droite et perpendiculaire incline un peu,
pour avoir été frappée de travers,
il faut la redresser en limant le cuivre sur le flanc de la matrice du côté opposé à l'endroit qui penche.
Dans cet exemple,
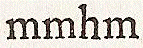 ,
où la lettre h penche à droite,
cet h doit être redressé en ôtant du cuivre à gauche vers la tête de la lettre ;
mais comme elle serait plus mince de ce côté,
et qu'il faut au contraire qu'elle soit d'égale épaisseur de haut en bas,
on en ôte autant de l'autre côté de la matrice par le bout opposé. ,
où la lettre h penche à droite,
cet h doit être redressé en ôtant du cuivre à gauche vers la tête de la lettre ;
mais comme elle serait plus mince de ce côté,
et qu'il faut au contraire qu'elle soit d'égale épaisseur de haut en bas,
on en ôte autant de l'autre côté de la matrice par le bout opposé. |
|
|
On sent
assez combien on doit employer
#de
précautions pour ne pas ôter trop de cuivre,
parce qu'il n'est plus possible d'en remettre.
Si cependant cet accident arrive,
pour la hauteur en papier,
on enfonce de nouveau le poinçon dans la matrice ; et quand on en a trop ôté sur les côtés,
on pique l'endroit avec un petit ciseau aigu,
ce qui produit de petites élévations : mais cette matrice sera
plus applatie que les autres entre les registres du moule,
elle sera par conséquent plutôt hors d'approche.
On remédiera à ce défaut d'approche par les registres du moule,
qui sont mobile exprès,
pour que l'on puisse redonner aux matrices plus ou moins applaties les différentes approches
qui leur conviennent.
Il faut donc,
à chaque matrice,
prendre garde à la hauteur en papier,
à la ligne,
à l'approche,
à la pente,
si c'est de l'italique,
à la perpendicularité pour le romain,
etc.
et n'y toucher que relativement à ces objets. |
|
|
Une première matrice
étant ainsi ébauchée,
on en prend une seconde,
après celle-ci une autre,
et ainsi de suite,
jusqu'à la fin du nombre que l'on fabrique à la fois ;
après quoi l'on fond de nouveau une lettre sur chacune,
et #on recommence l'opération peu à peu,
comme je viens de le dire,
jusqu'à ce qu'elles soient enfin dans la perfection recquise. |
|
|
La justification
des caractères italiques est plus difficile que celle des caractères romains,
parce que la pente n'est ordinairement guidée que par la vue,
au lieu que dans le romain la tige de la lettre,
qui est droite,
guide plus facilement l'œil.
Il faut prendre pour l'italique quelques précautions de plus,
qui consistent à justifier d'abord l'H ou l'I capital avec l'm ;
celle-ci sert pour guider la pente des lettres de même calibre,
et l'I ou l'H pour guider celle des longues,
telles que les b,
h,
l,
p, etc.
en présentant ces longues à côté de cet I,
à mesure qu'on les justifie,
et les réduisant au même degré d'inclinaison. |
|
|
Quand cela est fait,
il ne s'agit plus que de parer les matrices : cette opération consiste à faire à
chacune une entaille en dessous vis-à-vis de l'œil de la lettre ;
cette entaille se nomme talon de la matrice ; elle sert à fixer
l'archet du moule
que l'on appuie dessus ; on fait ensuite deux petits crans au haut de la matrice,
l'un dessus,
l'autre dessous,
au moyen desquels
#on attache
avec un fil un morceau de peau que l'on nomme attache. |
|
|
Pour parer
proprement les matrices,
afin qu'elles soient d'égale épaisseur de la face au talon,
et de même longueur,
ce qui présente un coup d'œil gracieux lorsqu'elles sont assemblées par frappes
dans leurs coulisses,
on fait un petit calibre de tôle,
taillé à l'extérieur comme une matrice.
Ce calibre,
nommé chappe,
est fermé par un bout,
et a par en bas un petit rebord, On pose la matrice du côté de l'œil
sur ce petit rebord, et après avoir serré l'une et l'autre dans l'étau,
on lime le dessous de la matrice au niveau de cette chappe en suivant
les entailles pour le talon et pour les crans ; cela fait,
on passe cette surface de la matrice en long sur une lime,
pour la polir ; puis avec une autre lime,
on abat légèrement tous les angles ; ensuite on enlève avec la pointe d'un canif les
bavures que la lime aurait pu chasser à l'orifice de la matrice,
ce qu'on appelle déchausser,
et par là se termine la justification de la matrice ; après quoi on les arrange par ordre
dans une boîte plate en forme de tiroir,
que l'on nomme frappe.
Chacune#
de ces boîtes contient toutes les matrices nécessaires à un caractère.
Elles ont été appelées frappes,
du nom de l'opération,
qui consiste à frapper le poinçon pour former la matrice :
de là on dit une frappe de Cicéro,
une frappe de Petit-romain,
etc.
quand la boîte contient les matrices propres à ces caractères.
Une frappe contient environ cent cinquante matrices pour les caractères,
soit romains,
soit italiques,
à savoir,
les lettres minuscules,
a, b, c, d, e, f,
etc. les lettres doubles,
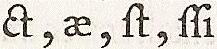 ;
les ponctuations . , : etc
les lettres accentuées, á, à, â, etc.
les grosses capitales, ;
les ponctuations . , : etc
les lettres accentuées, á, à, â, etc.
les grosses capitales, 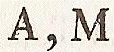 , etc.
les petites capitales, , etc.
les petites capitales, 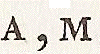 , etc.
et les chiffres,
dont on verra le détail par la police qui se trouvera
ci-après.
Les frappes de grec contiennent six à sept cents matrices,
plus ou moins,
suivant le nombre plus ou moins étendu des abbréviations,
que l'on nomme ligatures,
parce que ce sont des lettres liées ensemble qui servent à former des mots soit entiers,
soit abrégés.
Les autres caractères contiennent chacun un nombre de matrices proportionné à leur
nature. , etc.
et les chiffres,
dont on verra le détail par la police qui se trouvera
ci-après.
Les frappes de grec contiennent six à sept cents matrices,
plus ou moins,
suivant le nombre plus ou moins étendu des abbréviations,
que l'on nomme ligatures,
parce que ce sont des lettres liées ensemble qui servent à former des mots soit entiers,
soit abrégés.
Les autres caractères contiennent chacun un nombre de matrices proportionné à leur
nature. |
|
|
Voilà tout
l'art du graveur rempli, et s'il
#a eu le bonheur de réussir,
son ouvrage peut passer à la postérité la plus reculée dans le même point de perfection,
sans jamais se corrompre ni s'altérer,
parce qu'après avoir fait un long usage des matrices,
on pourra les faire renaître de nouveau par le moyen des mêmes poinçons ;
en cela bien plus heureux que le graveur en taille-douce,qui,
après l'impression de deux ou trois milliers d'estampes,
est obligé de retoucher sa planche,
et enfin de l'abandonner comme inutile.
Les caractères de fonte,
au contraire,
renaissent comme d'eux-mêmes,
et sont reproduits à l'infini pendant des siècles entiers par l'art de la fonderie,
dont nous allons voir le détail. |
|
|

|
|
 XIII
XIII