|
Juillet 2006 : cette page était initialement (1998) sur le site http://www.irisa.fr/faqtypo/truchet.html.
http://jacques-andre.fr/faqtypo/truchet/truchet.html |
|
|
Truchet & Types par
Cette note a été écrite pour le congrès AtypI (Association TYpographique Internationale) de 1998 qui s'est tenu à Lyon où est né, en 1657, le Père Sébastien Truchet. C'était pour nous l'occasion de réhabiliter la mémoire de ce Père Sébastien Truchet. Si celui-ci est en effet connu comme mathématicien (son nom reste notamment attaché aux « pavages de Truchet »), comme spécialiste en hydraulique (on lui doit la majorité des canaux français) et comme l'inventeur d'un nombre incoroyable de choses (depuis des cadrans solaires jusqu'à des canons en passant par des machines pour transplanter des arbres adultes, machines utilisées pour « planter » le parc du château de Versailles), peu de typographes savent qu'on lui doit l'invention du point typographique et qu'il a participé à la conception du célèbre Romain du roi.
Voici donc trois histoires de son apport à la typographie : |
|
En cette fin du XVIIe siècle,
les forces de corps ne se mesuraient pas : on leur donnait des noms (tout comme aujourd'hui encore,
on nomme les graisses : gras,
maigre,
demi gras sans qu'il y ait vraiment de mesure). Ces noms étaient souvent basés sur ceux des livres où ces caractères avaient été employés la première fois. Par exemple,
on désignait par « Cicéro » la force des caractères utilisés pour les Épîtres de Cicéron ou par « Saint Augustin »
celle des caractères composant la Cité de Dieu de ce Père de l'Église. Ils pouvaient aussi
venir de leur allure :
le « pica » anglais par exemple vient du latin pica
(la pie) car le premier livre imprimé ainsi utilisait des noirs et blancs très tranchés,
comme le plumage de cet oiseau ! D'autres noms sont issus soit de l'origine des caractères (par exemple « Parisienne »),
soit de leur fonction (« Canon » français,
« brevier » anglais ou « Missal » allemand),
soit de leur taille relative (« Petit-Romain »,
« Gros-Canon ») car il y avait une échelle implicite entre ces forces (un « Petit canon » par exemple étant deux fois plus grand qu'un « Saint-Augustin »). Mais d'une fonderie à l'autre,
les tailles variaient énormément et il était très difficile de mélanger les types de fonderies différentes,
voire d'une même fonderie ! Cette fin du XVIIe siècle, c'est aussi le siècle des Lumières. Jaloux de voir ce qui se faisait à l'étranger, le ministre de Louis XIV, Colbert, décide, en 1692, de faire préparer une collection de recueils sur les arts et métiers et nomme quatre savants à la tête de ce travail : l'abbé Bignon, Jacques Jaugeon, Gilles Filleau des Billettes et le Père Sébastien Truchet. Ils se mirent au travail et rapidement plusieurs descriptions, illustrées, de métiers furent prêtes. En 1699, Louis XIV les fit entrer à l'Académie et ils continuèrent leur travail sous la direction de Réaumur. Mais en 1750 (Truchet était déjà mort !), alors qu'aucun tome de la Description des métiers n'était encore paru, Diderot et D'Alembert annoncent leur Encyclopédie ce qui vexe l'Académie qui publie alors soixante-treize volumes et près de deux mille planches. Les collections de cette Description des métiers sont très rares et cette œuvre est complètement méconnue ! Revenons à 1693, quand la commission Bignon démarre son travail et décide de commencer par décrire les métiers par « l'art qui conservera tous les autres, c'est-à-dire l'impression ». Cette commission, et notamment Truchet, étudie (avec même l'emploi d'un de ces microscopes qui venaient d'être inventés) les caractères connus à l'époque et propose trois projets successifs de systèmes de quantification des types où la succession des corps est liée à des incréments réguliers, basés sur la « ligne », une unité d'orfèvrerie qui valait 1/12 du pouce officiel : on n'est qu'au XVIIe siècle et le système métrique n'est pas encore adopté, même si en 1670 le père Mouton proposa déjà à l'Académie une unité de longueur, la virga, égale à la millième partie de la distance découpée sur le méridien terrestre par une minute d'angle. Les unités de longueur à l'époque comprennent notamment la toise formée de 2 aulnes (à peu près notre mètre) formés de 3 pieds ; le pied (0, 32484m) était divisé en 12 pouces (2,707 cm), chaque pouce était divisé en 12 lignes (de 2, 256mm) et chaque ligne en 12 points métriques (de 0, 188mm). Le problème est que ces valeurs variaient d'un lieu à l'autre, celles données ici étant celles dites du roi. Bien sûr, pieds et pouces anglais étaient légèrement différents ! Le premier projet date de 1694. Il repose sur quelques principes :
Nous donnons cette dernière règle ici en termes mathématiques modernes :
Le second projet, en 1695, était basé sur 1/24 de ligne, mais le troisième utilisa une unité beaucoup plus petite, le 1/204 de ligne, soit aujourd'hui 0,011057mm. Ceci correspond donc en gros à une définition de 2300 dpi ! Si cette valeur nous fait rêver, elle fait toujours rire les graveurs de poinçons car aucun outil mécanique ne permet de respecter cette précision. Fournier, 50 ans plus tard, emploiera 7 parties là où Truchet en propose 204 et dit « Ces règles renvoient à l'idée des infiniment petits, où l'imagination seule peut atteindre Faut-il donc tant de carrés pour former un O qui est rond ? » (Manuel typographique page xvj). Cette valeur surprenante de 204 est peut-être liée au produit de 12 × 17, où 12 est bien sûr la base duodécimale et où 17 pourrait être égal au nombre de lignes (16) que l'on trouve dans les dessins des bas de casse gravées par Simoneau plus 2/2 (deux demi lignes pour les talus).
Mais, cette invention n'a pas eu de suite immédiate. Sans doute était-elle « trop académique » ? Il aurait fallu re-graver tous les poinçons et re-fabriquer tous les types ! D'ailleurs, le système qu'il proposait n'étant pas exactement identique à celui utilisé alors (c'est-à-dire que la rigueur de son système ne décrivait pas exactement la réalité, déformée, de l'époque), Truchet inventa de nouveaux noms pour les forces de caractères, tels que « La Petite Royale » (corps 12), « Le Bourbon » (corps 36), etc. |
|
Par ailleurs, les membres de la Chambre syndicale des imprimeurs ne connurent probablement pas ces recherches car ils firent proposer par le roi une Ordonnance (datée du 28 février 1723) précisant la hauteur en papier des types, amis aussi les rapports officiels entre les anciennes appellations ! Pierre-Simon Fournier, dit le Jeune, lui, connût les travaux de Truchet (puisqu'il s'en moquât) et reprit l'idée de proportions, mais cette fois en adaptant l'échelle aux corps existants. C'est le point Fournier de 1737, malheureusement pas basé sur une unité légale ! Notons que le point Fournier était plus proche du pica que de celui de Truchet. Didot à son tour reprit l'idée de Truchet et normalisa le point en 1783 (basé sur le 1/72 du pouce français mais avec pratiquement les mêmes progressions que Truchet). Comme pour le point de Truchet, il fallu re-graver des poinçons ce qui explique que nombre d'imprimeurs soient restés jusqu'au XXe siècle avec le point Fournier !
|
|
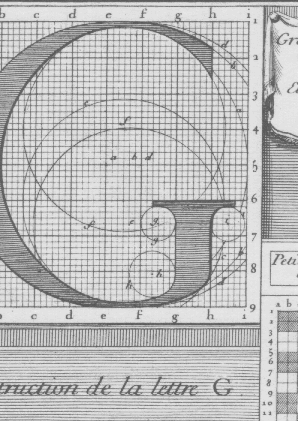
On a vu dans la section précédente que le père Sébastien Truchet a été nommé par Louis XIV pour participer aux travaux de la Commission Bignon en vue de la préparation d'une encyclopédie sur les métiers, le premier qu'ils étudient étant celui d'imprimeur ! La commission se met alors à étudier les caractères existants et trois membres (Truchet, Jaugeon et Des Billettes) se lancent dans la conception « de nouvelles lettres françaises, que l'on a tâché de rendre les plus agréables à l'œil qu'il fût possible. » Ces caractères rompent avec la tradition du Garamond et leur originalité a été expliquée par Stanley Morison puis André Jammes : ce sont des caractères influencés par l'idée que « l'imprimerie n'est pas une branche de l'écriture mais de la gravure. » Or justement, ce qu'ont produits ces trois académiciens, ce sont ces caractères des planches (gravées par Simoneau) du Romain du roi et que Grandjean utilisera pour faire les poinçons des caractères qui ont notamment servis à composer l'ouvrage Médailles sur les principaux événements du règne de Louis le grand en 1702. (N.B. Ce caractère a récemment été numérisé par Franck Jalleau sous le nom de Grandjean-IN). Bien qu'habituellement attribué à Jaugeon (le seul membre de la commission Bignon qui fût de culture typographique), l'apport du « mécanicien » qu'était Truchet est sûrement prépondérante. D'ailleurs les manuscrits conservés sont tous de la main de Truchet (voir table des corps). On doit leur étude à André Jammes et à James Mosley. Mais si les planches de Simoneau ont souvent été reproduites, les notes manuscrites de Truchet sont méconnues. Or ce sont l'équivalent des AFM (Font Metrics) d'aujourd'hui, voire des instructions de hinting !
Nous ne pouvons nous empêcher d'insister sur le génie de ces chercheurs d'il y a trois cents ans.
Le Romain du roi a tout d'une fonte numérique d'aujourd'hui, mais elle a 300 ans !
|
|
Après sa participation à la commission Bignon qui le menèrent à la définition du point typographique et à la conception géométrique du Romain du roi, le Père Truchet retourne, début 1700, à ce qui aura été sa spécialité principale : l'hydraulique. Il travaille alors au projet du Canal d'Orléans et voit dans un Château nommé la Motte S. Lyé, à 4 lieuës en deçà d'Orleans plusieurs Carreaux de fayence quarrés & mipartis de deux couleurs par une ligne diagonale , qui étoient destinez à carreler une Chapelle & plusieurs autres appartements. Truchet cherche alors le moyen de combiner ces pavés pour en faire des dessins plaisants et publie en 1704 le résultat de ses recherches dans les Comptes-rendus de l'Académie des Sciences. Cette notion de pavage n'était pas nouvelle mais l'apport de Truchet, c'est d'avoir fait la première publication d'une étude systématique de toutes les combinaisons d'un pavage.
En réalité, rien n'est plus commun, puisqu'il suffit d'en être averti pour en découvrir partout, depuis les murs de nos salles de bain et le dallage de nos cuisines jusqu'à certains décors de monuments et d'églises, en passant par les ruches des abeilles ou certains vêtements... Là comme ailleurs, il a fallu que les mathématiciens s'intéressent à ce domaine, en l'espèce à partir du milieu du XIXe siècle, pour que des définitions précises et des classifications soient établies, bref pour constituer ces questions en une théorie. Mais la définition intuitive est suffisante pour cerner ce que recouvre le concept de « pavage » : composition d'une surface par assemblage de pièces élémentaires, sans laisser d'espaces libres et en évitant tout recouvrement, et ceci avec un nombre très réduit de types différents de pièces (parfois un seul – pensons encore une fois aux carreaux de nos salles de bains ou aux alvéoles des nids d'abeilles). Ce principe rudimentaire se révèle néanmoins extrêmement riche, notamment si on combine ensemble plusieurs types de pièces et si on les colorie en respectant un certain ordre. On peut ainsi obtenir des résultats fort agréables à l'œil, voire tout à fait fascinants. C'est pourquoi depuis l'aube des temps jusqu'à aujourd'hui, et dans toutes les civilisations, les artisans et les décorateurs ont beaucoup joué sur ces effets, les artistes arabes ayant en particulier atteint en la matière une maîtrise stupéfiante, qui ne sera retrouvée à l'époque moderne que par le célèbre graveur Escher, car l'interdiction propre à leur religion de représenter des êtres animés les a poussé à chercher à produire par le seul moyen de la géométrie des décorations variées et séduisantes. Mais si de tels effets plaisent à l'œil, c'est seulement parce qu'ils obéissent à des lois mathématiques précises, même bien sûr aux époques où on les appliquait avant qu'elles aient été découvertes ! Ce fut là en réalité un domaine où la pratique a pris un bon nombre de siècles d'avance sur la théorie ! Certes, les savants grecs avaient déjà établis en leur temps quelques résultats simples et, plus important encore, avaient compris certains enjeux essentiels, en voyant notamment que la réponse à la question de la structure discrète ou bien continue de la matière, objet d'une célèbre controverse entre Platon et Aristote connue sous le nom de « querelle de l'atomisme », est liée à des considérations de remplissage de l'espace à l'aide de volumes réguliers, généralisation au cas de l'espace d'un problème de pavage du plan. Mais ces questions ne seront quasiment pas reprises avant l'époque moderne, sauf par quelques pionniers, tel notamment le grand astronome Kepler qui y consacra au début du XVIIe siècle des recherches longues et fructueuses, mais dont les résultats furent complètement oubliés pendant trois cents ans ! Et parmi ces premiers découvreurs, on trouve donc aussi, comme on l'a dit, le Père Truchet. Mais ce n'est qu'à la fin du XIXe siècle, sous l'impulsion essentielle de la cristallographie, que les mathématiciens se sont intéressés à ces problèmes, en utilisant notamment la théorie des groupes fondée quelques décennies plus tôt par Gallois. Car un fait majeur dont on prit progressivement conscience et qui devint patent au début de notre siècle, c'est que « la géométrie des pavages est à la base de toute structure atomique ». Les cristallographes et les mathématiciens ont donc tout au long du siècle, par une sorte d'auto-fécondation réciproque, fait grandement avancer la théorie des pavages. Ainsi c'est elle qui, au milieu des années 80, a fourni après coup la clé de la compréhension de l'existence des quasicristaux, ces entités qu'on pensait jusqu'alors inexistantes car impossibles. Toutefois, dans ce domaine aussi riche que complexe, beaucoup de questions restent en suspens, même certaines dont la formulation tient pourtant en une ligne... Néanmoins, des résultats de la théorie des pavages sont par contre utilisés aujourd'hui dans des domaines très variés, de l'informatique théorique au traitement d'images, de la micro-typographie à la physique statistique, de la biologie à la génération de maillages pour la modélisation numérique. Là encore, le Père Truchet a donc été un précurseur de premier ordre, mais oublié. Aussi revenons à lui... ou plutôt à Fournier : Truchet ayant été appelé à travailler au projet du Parc de Versailles, son travail sera repris quelques années plus tard par un autre religieux, le Père dominicain Douat, qui publie un livre (Méthode pour faire une infinité de desseins différents) dont Fournier aura connaissance plusieurs dizaines d'années plus tard. Fournier, ancien graveur sur bois, s'est intéressé aux vignettes qui jusque là étaient surtout gravées sur bois. Son apport est triple :
En fait, à part quelques pages de son Manuel, il ne semble pas qu'il y ait eu de nombreuses utilisations de ces vignettes pour faire des « pavages ». Par contre, le principe de base des pavés de Truchet (carré dont le dessin est très marqué par une diagonale) se retrouve dans les vignettes de Luce et du Manuel de Fournier (165 vignettes dont 1/3 présentent cette symétrie), qui seront largement reprise par Bodoni, Caslon et autres Peignot. Signalons que l'emploi de ces vignettes pour faire des frises relève de ce qu'on appelle les groupes de frises (proche des groupes de symétrie des cristallographes). La simple juxtaposition de vignettes pour faire des tarots (dos de cartes à jouer, comme ceux de Rosart au XVIIIe siècle) ne peut vraiment être assimilée à un pavage de Truchet. En revanche, on trouve des tarots (probablement gravés sur cuivre) qui eux relèvent des pavages de Truchet, comme celui ci-dessous et d'autres des fonderies Laurent et Deberny ou Peignot.
Aujourd'hui les fontes modernes offrent des woodornaments et fleurons qui ne sont pas assez utilisés dans cet esprit ; pourtant à partir d'une vignette de base, il est facile de créer un grand nombre de pavages de Truchet (figure ci-dessous) par simple composition « géométrique ». Leur « programmation » est très aisée à l'aide de langages comme PostScript ou pst-fill.
|
|
|
|
Haut de la page
Truchet
Point typographique
Romain du roi Pavages |
|
Aller aux pages : Truchet (et Doüat), Ornements & pavages, FAQ Typo |
 An English version is available as a TUGBOAT
paper
An English version is available as a TUGBOAT
paper